BOLCHEM
Model description
The on-line coupled meteorology-chemistry model BOLCHEM (Bologna limited area model for meteorology and chemistry)
is based on the BOLAM meteorological model.
The chemistry is integrated simultaneously with meteorology without any interpolation in time or space.
BOLAM dynamics is based on hydrostatic primitive equations, with wind components u and v, potential
temperature 
, specific humidity q, surface pressure ps, as dependent
variables. The vertical coordinate system is terrain-following 
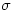, with variables
distributed on a non-uniformly spaced staggered Lorenz grid. The horizontal
discretization uses geographical coordinates on an Arakawa C-grid. The
time scheme is split-explicit, forward-backward for gravity modes. A 3-d WAF
(Weighted Average Flux) advection scheme coupled with semi-Lagrangian advection
of hydrometeors is implemented. A fourth order horizontal diffusion
of the prognostic variables (except for ps), a second order divergence diffusion
and damping of the external gravity mode are included. The cumulus parameterization is based on
the Kain-Fritsch scheme (Kain and Fritsch, 2006) that uses a sophisticated
cloud-mixing scheme to determine entrainment and detrainment.
The 3-d advection of pollutants is done by means of the same mass-conservative
WAF-based scheme used for the meteorological quantities.
The chemical transformations of the tropospheric gases can be described by means of two photochemical mechanisms:
Carbon-Bond Mechanism version IV (CB-IV) (Gery et al., 1989) and SAPRC90 (Carter,1990).
CB-IV mechanism represents the emissions by 30 chemical species that undergo 85 reactions, while
SAPRC90 mechanism represents the emissions by 35 chemical species that undergo 131 reactions.
The dry deposition scheme included in BOLCHEM follows the resistance analogy approach (Wesley, 1989) with
the deposition velocity (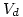
) function of three resistance terms: the aerodynamic resistance (
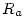), the quasi laminar resistance (
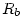) and surface resistance (
).
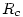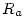is computed using the friction velocity and the Businger stability functions at
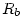the surface layer; is computed in different ways over land and sea: over the land,
the friction velocity is scaled according to the diffusivity characteristics of the gas (Hicks et al.,1987)
and over the sea, is approximated by the procedure presented by (Hicks et al., 1976).
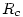considered only specie's dependent.
Technical details can be found at the COST 728/732 Model Inventory web page.
References
Kain, J. S. and Fritsch, J. M. (2006). Convective parameterization for mesoscale models: the kain-fritsch scheme: the representation of cumulus numerical models. In: Emanuel, K. A. Raymond, D. J. (Eds), Meteorological Monographs. American Meteorological Society, 165-170.
Carter, W. P. L. (1990). A detailed mechanism for the gas-phase atmospheric reactions of organic compounds. Atmos. Environ., 27A, 481-518.
Gery, M. W., Witten, G. Z., Killus, J. P. and Dodge, M. C. (1989). A photochemical kinetics mechanism for urban and regional scale computer modeling. J. Geophys. Res., 94(D10), 12925-12956.
Hicks, B. B., Baldocchi, D. D., Meyers, T. P., Hosker R.D. and Matt, D. R. (1987). A preliminary multiple resistance routine for deriving dry deposition velocities from measured quantities. Water, Air and Soil Pollution, 36, 311-330.